Menentukan Resultan Vektor dengan Penguraian Vektor

Postingan tentang menentukan resultan vektor dengan penguraian vektor ini merupakan lanjutan dari postingan sebelumnya tentang bagaimana cara menguraikan sebuah vektor menjadi komponen-komponennya. Kita ketahui bahwa dalam koordinat (x, y) sebuah vektor dapat diuraikan dua vektor komponen yaitu vektor komponen sumbu x dan vektor komponen sumbu y.

Dengan menggunakan metode penguraian vektor maka kita akan dapat menentukan besar dan arah resultan dari beberapa vektor yang jumlahnya lebih dari dua buah vektor. Metode penguraian vektor sering dikenal dengan istilah metode analisis. Bagaiamana cara mencari besar dan arah resultan vektor dengan metode penguraian (metode analisis)?

Perhatikan gambar 1 di bawah ini.

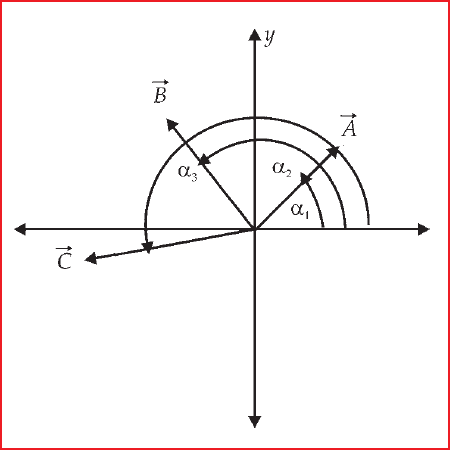Gambar 1

Gambar 1 di atas terdapat tiga buah vektor yaitu vektor A membentuk sudut α₁tehadap sumbu x, vektor B membentuk sudut α₂ tehadap sumbu x, dan vektor C membentuk sudut α₃ tehadap sumbu x. Jika masing-masing dari ketiga vektor tersebut diuraikan maka akan tampak seperti gambar 2 di bawah ini.

Gambar 2

Dengan menguraikan masing-masing vektor maka kita akan dapatkan komponen-komponennya, yakni:

Untuk vektor A, maka vektor komponennya:

A_x = A cos α₁

A_y = A sin α₁

Untuk vektor B, maka vektor komponennya:

B_x = B cos α₂

B_y = B sin α₂

Untuk vektor C, maka vektor komponennya:

C_x = C cos α₃

C_y = C sin α₃

Dengan menjumlahkan masing-masing komponen berdasarkan sumbunya maka diperoleh jumlah komponen pada sumbu x (Rx) dan pada sumbu y (Ry) yakni:

Rx = Ax + Bx + Cx

Ry = Ay + By + Cy

Untuk mencari besar resultan vektornya dapat menggunakan rumus:

          R²= Rx² + Ry²

atau

          R = √(Rx² + Ry²)

Sedangkan untuk mencari arah vektor resultan terhadap sumbu x positif dapat dihitung dengan persamaan:

          Tan α = Ry/Rx

Untuk memantapkan pemahaman Anda mengenai cara menentukan besar dan arah resultan vektor dengan cara penguraian vektor atau metode analisis, silahkan perhatikan contoh soaldi bawah ini.

Contoh Soal

Empat buah vektor gaya yang memiliki titik pangkal berimpit dengan besar 20 N, 12 N, 10 N, dan 14 N. Keempat vektor tersebut membentuk sudut terhadap sumbu x masing-masing 0°, 60°, 120° dan 240°. Hitunglah besar dan arah resultan keempat vektor tersebut.

Penyelesaian:

Diketahui:

F₁= 20 N, α₁ = 0°

F₂= 12 N, α₂ = 60°

F₃= 10 N, α₁ = 120°

F₄= 14 N, α₁ = 240°

Jika digambarkan akan tampak seperti Gambar 3 di bawah ini.

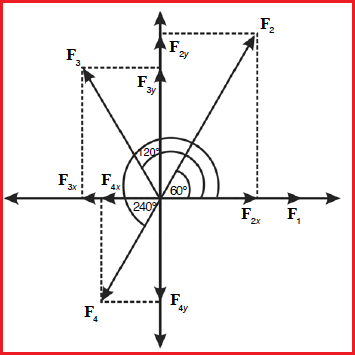Gambar 3

Dengan menggunakan konsep cara menguraikan vektor maka masing-masing vektora kan diperoleh komponen-komponennya, yakni:

F_1x = F₁ cos 0° = 20 N . 1 = 20 N

F_1y = F₁ sin 0° = 20 N . 0 = 0

F_2x = F₂ cos 60° = 12 N . ½ = 6 N

F_2y = F₂ sin 60° = 12 N . ½√3  = 6√3 N

F_3x = F₃ cos 120° = 10 N . – ½ = – 5 N

F_3y = F₃ sin 120° = 10 N . ½√3 = 5√3 N

F_4x = F₄ cos 240° = 14 N . – ½ = – 7 N

F_4y = F₄ sin 240° = 14 N . –½√3 = –7√3 N

Jumlah vektor komponen sumbu x yakni:

F_Rx = F_1x + F_2x+ F_3x + F_4x

F_Rx = 20 N + 6 N + – 5 N + – 7 N

F_Rx = 14 N

Jumlah vektor komponen sumbu y yakni:

F_Ry = F_1y + F_2y+ F_3y + F_4y

F_Ry = 0 + 6√3 N + 5√3 N + –7√3 N

F_Ry = 4√3 N

Besar resultan dari keempat vektor tersebut yakni:

F_R = √(F_Rx² + F_Ry²)

F_R = √(14² + [4√3]²)

F_R = √(196 + 48)

F_R = √244

F_R = 15,6 N

Arah resultan dari keempat vektor tersebut yakni:

Tan α = F_Ry/F_Rx

Tan α = 4√3 N/14 N

Tan α = 0,5

α = arc tan 0,5

α = 26,5°

Jadi, besar dan arah resultan keempat vektor tersebut adalah 15,6 N dan 26,5° terhadap sumbu x.

Demikian postingan Mafia Online tentang cara menentukan besar dan arah resultan vektor dengan cara menguraikan vektor (metode analisis) dan juga contoh soalnya. Mohon maaf jika ada kata atau perhitungan yang salah dalam postingan ini. Salam Mafia => Kita pasti bisa.