Contoh Soal dan Pembahasan Panjang Sabuk Lilitan Minimal Pada Lingkaran

Syarat untuk agar mampu menentukan panjang sabuk lilitan minimal yang menghubungkan dua lingkaran atau lebih adalah Anda harus menguasai konsep dasar tentang lingkaran yaitu keliling lingkarandan hubungan antara sudut pusat dengan panjang busur suatu lingkaran. Kalau anda sudah menguasai konsep tersebut silahkan anda pelajari pembahasan soal-soal tentang Menentukan Panjang Sabuk Lilitan Minimal Yang Menghubungkan Dua Lingkaran atau lebih berikut ini. 

Pembahasan Soal Latihan Tentang Menentukan Panjang Sabuk Lilitan Minimal Yang Menghubungkan Dua Lingkaran atau Lebih

Contoh Soal 1

Gambar di bawah adalah penampang tiga buah pipa air yang berbentuk tabung dengan diameter 14 cm. Berapakah panjang tali minimal untuk mengikat tiga buah pipa dengan susunan tersebut?

Penyelesaian: 

 

Diketahui bahwa diameter lingkaran adalah 14 cm, maka jari-jarinya adalah 7 cm. Hubungkan titik pusat ketiga lingkaran dan titik pusat dengan tali yang melingkarinya, seperti pada gambar di atas, sehingga diperoleh:

panjang AB = EF = DC = 4 x jari-jari = 28 cm. 

Ingat kembali materi pada bab sebelumnya mengenai lingkaran, bahwa keliling lingkaran adalah 2πr, dalam hal ini panjang busur lingkaran AD merupakan ½ lingkaran. Maka:

panjang busur AD = busur BC = ½ keliling lingkaran = πr = 22 cm

Panjang tali minimal untuk mengikat tiga buah pipa dengan susunan tersebut adalah:

panjang tali  = 2 x panjang AB + 2 x panjang busur AD

panjang tali  = 2 x 28 cm + 2 x 22 cm

panjang tali  = 100 cm

Jadi panjang tali minimal untuk mengikat tiga buah pipa dengan susunan tersebut 100 cm

Contoh Soal 2

Dua buah kayu berpenampang lingkaran diikat dengan tali yang panjangnya 144 cm. Jika jari-jarinya sama panjang maka tentukan panjang jari-jari kedua kayu.

Penyelesaian: 

 

Misalkan jari-jari lingkaran kayu tersebut adalah r. Hubungkan titik pusat kedua lingkaran dan titik pusat dengan tali yang melingkari kayu, seperti pada gambar di atas, sehingga diperoleh:

panjang AB = EF = DC = 2 x jari-jari = 2r

Ingat kembali materi pada bab sebelumnya mengenai lingkaran, bahwa keliling lingkaran adalah 2πr, dalam hal ini panjang busur lingkaran AD merupakan ½ lingkaran. Maka:

panjang busur AD = busur BC = ½ keliling lingkaran = πr

Panjang tali minimal untuk mengikat dua buah kayu dengan susunan tersebut adalah:

panjang tali = 2 x panjang AB + 2 x panjang busur AD

 panjang tali = 2 (panjang AB + panjang busur AD)

144 cm = 2 (2r + πr) <= sama-sama dibagi 2, maka

72 cm = 2r + πr

72 cm = 2r + (22/7)r

72 cm = (14/7)r + (22/7)r

72 cm = (36/7)r

r = 72 cm x 7/36

r = 14 cm

Jadi, panjang jari-jari kedua kayu adalah 14 cm

Contoh Soal 3

Gambar di bawah adalah penampang enam buah drum yang berbentuk tabung dengan jari-jari 28 cm. Hitunglah panjang tali minimal yang diperlukan untuk mengikat enam buah drum tersebut.

Penyelesaian: 

 

Diketahui bahwa jari-jari drum adalah 28 cm. Hubungkan titik pusat enam lingkaran drum dan titik pusat dengan tali yang melingkarinya, seperti pada gambar di atas, sehingga diperoleh:

panjang IH = DE = FG = 4 x jari-jari = 112 cm.

Segitiga ABC sama sisi, sehingga

∠ ABC = ∠ BAC = ∠ ACB = 60°;

∠IAC = ∠DAB = 90° (siku-siku);

∠DAI = ∠HCG = ∠EBF = 360° – (60° + 90° + 90°) =120° 

Ingat kembali materi pada bab sebelumnya mengenai hubungan sudut pusat dengan panjang busur lingkaran, maka:

panjang busur ID/ keliling lingkaran = (∠DAI/360°)

panjang busur ID/ 2πr = (∠DAI/360°)

panjang busur ID = (120°/360°) x 2πr

panjang busur ID = (1/3) x 2πr

panjang busur ID = (1/3) x 2 x (22/7) x 28 cm

panjang busur ID = (176/3) cm 

Jadi, panjang tali minimal untuk mengikat enam buah drum dengan susunan tersebut adalah:

panjang tali  = 3 x panjang IH + 3 x panjang busur ID

panjang tali  = 3 x 112 cm + 3 x (176/3) cm

panjang tali  = 336 cm + 176 cm

panjang tali  = 512 cm

Jadi, panjang tali minimal yang diperlukan untuk mengikat enam buah drum tersebut adalah 512 cm

Pembahasan Soal 4

Gambar di bawah adalah penampang enam buah kaleng yang berbentuk tabung dengan jari-jari 10 cm. Hitunglah panjang tali minimal yang diperlukan untuk mengikat enam buah kaleng tersebut.

Penyelesaian: 

 

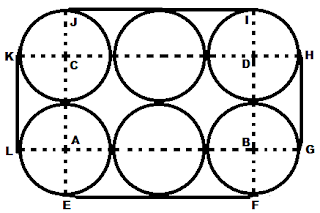Diketahui bahwa jari-jari kaleng adalah 10 cm. Hubungkan titik pusat enam lingkaran kaleng dan titik pusat dengan tali yang melingkarinya, seperti pada gambar di atas, sehingga diperoleh:

panjang EF = IJ = 4 x jari-jari = 40 cm, dan

panjang KL = GH = 2 x jari-jari = 20 cm

Ingat kembali materi pada bab sebelumnya mengenai lingkaran, bahwa keliling lingkaran adalah 2πr, dalam hal ini panjang busur lingkaran AD merupakan ¼ lingkaran. Maka:

panjang LE = FG = HI = JK

panjang LE = ¼ keliling lingkaran

panjang LE = ½πr

Jadi, panjang tali minimal untuk mengikat enam buah drum dengan susunan tersebut adalah:

panjang tali  = 2 x EF + 2 x KL + 4 x panjang busur LE

panjang tali  = 2 x EF + 2 x KL + 4 x ½πr

panjang tali  = 2 x 40 cm + 2 x 20 cm + 2 x 3,14 x 10 cm

panjang tali  = 80 cm + 40 cm + 62,8 cm

panjang tali  = 182,8 cm

Jadi, panjang tali minimal yang diperlukan untuk mengikat enam buah kaleng tersebut adalah 182,8 cm

Pembahasan Soal 4

Lima buah pipa air disusun seperti pada gambar di bawah. Hitunglah panjang tali yang digunakan untuk melilitkan pipa-pipa tersebut jika jari-jari pipa 3 cm.

Penyelesaian: 

 

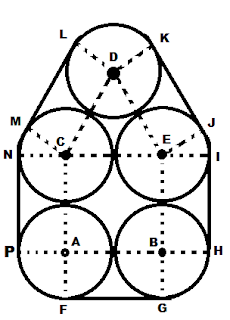Diketahui bahwa jari-jari pipa adalah 3 cm. Hubungkan titik pusat lima lingkaran pipa dan titik pusat dengan tali yang melingkarinya, seperti pada gambar di atas, sehingga diperoleh:

panjang FG = HI = JK = LM = NP = 2 x jari-jari = 6 cm.

Ingat kembali materi pada bab sebelumnya mengenai lingkaran, bahwa keliling lingkaran adalah 2πr, dalam hal ini panjang busur lingkaran AD merupakan ¼ lingkaran. Maka:

panjang GH = FP

panjang GH = ¼ keliling lingkaran

panjang GH = ½πr

panjang GH = ½ x 3,14 x 3 cm

panjang GH = 4,71 cm

Segitiga CDE sama sisi, sehingga

∠ CED = ∠ EDC = ∠ DCE = 60°;

∠KDE = ∠LDC = 90° (siku-siku);

∠KDL = 360° – (60° + 90° + 90°) =120°

∠MCN = ∠IEJ = 360° – (60° + 90° + 90° + 90°) = 30°

Ingat kembali materi pada bab sebelumnya mengenai hubungan sudut pusat dengan panjang busur lingkaran, maka:

panjang busur KL/ keliling lingkaran = (∠KDL/360°)

panjang busur KL / 2πr = (∠KDL/360°)

panjang busur KL = (120°/360°) x 2πr

panjang busur KL = (1/3) x 2πr

panjang busur KL = (1/3) x 2 x 3,14 x 3 cm

panjang busur KL = 6,28cm

sedangkan panjang busur IJ adalah:

panjang busur IJ/ keliling lingkaran = (∠IEJ/360°)

panjang busur IJ / 2πr = (∠IEJ /360°)

panjang busur IJ = (30°/360°) x 2πr

panjang busur IJ = (1/12) x 2πr

panjang busur IJ = (1/12) x 2 x 3,14 x 3 cm

panjang busur IJ = 1,57cm

Jadi, panjang tali minimal untuk mengikat enam buah drum dengan susunan tersebut adalah:

panjang tali  = 5 x FG + 2 x GH + KL + 2x IJ

panjang tali  = 5 x 6 cm + 2 x 4,71 + 6,28 cm + 2 x 1,57cm

panjang tali  = 30 cm + 9,42 cm + 6,28cm + 3,14 cm

panjang tali  = 48,84 cm

Jadi, panjang tali yang digunakan untuk melilitkan pipa-pipa tersebut adalah 48,84 cm
 

Mau cara cepat? Silahkan baca “Cara Cepat Menghitung Panjang Sabuk Lilitan Minimal Pada Lingkaran”