Pasangan Sudut yang Saling Berpelurus (Bersuplemen)
Perhatikan gambar di bawah.
 Garis AB merupakan garis lurus, sehingga besar ∠AOB = 180°. Pada garis AB, dari titik O dibuat garis melalui C, sehingga terbentuk ∠AOC dan ∠BOC.
Garis AB merupakan garis lurus, sehingga besar ∠AOB = 180°. Pada garis AB, dari titik O dibuat garis melalui C, sehingga terbentuk ∠AOC dan ∠BOC.
∠AOC merupakan pelurus atau suplemen dari ∠BOC. Demikian pula sebaliknya, ∠BOC merupakan pelurus atau suplemen ∠AOC, sehingga diperoleh:
Perhatikan gambar di bawah.

∠AOC merupakan pelurus atau suplemen dari ∠BOC. Demikian pula sebaliknya, ∠BOC merupakan pelurus atau suplemen ∠AOC, sehingga diperoleh:
∠AOC + ∠BOC = ∠AOB
a° + b° = 180°
atau dapat ditulis:
a° = 180° – b° atau
b° = 180° – a°.
Dari uraian di atas dapat disimpulkan sebagai berikut. Jumlah dua sudut yang saling berpelurus (bersuplemen) adalah 180°. Sudut yang satu merupakan pelurus dari sudut yang lain.
Dari uraian di atas dapat disimpulkan sebagai berikut. Jumlah dua sudut yang saling berpelurus (bersuplemen) adalah 180°. Sudut yang satu merupakan pelurus dari sudut yang lain.
Contoh Soal
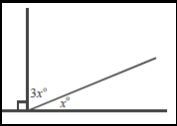
Perhatikan gambar di bawah ini.
 Hitunglah nilai a° dan tentukan pelurus dari sudut a°.
Hitunglah nilai a° dan tentukan pelurus dari sudut a°.

Penyelesaian:
Berdasarkan gambar diperoleh bahwa
3a° + 2a° = 180°
5a° = 180°
a° = 180°/5
a° = 36
Pelurus sudut a° = 180° – 36° = 144°.
Pasangan Sudut yang Saling Berpenyiku (Berkomplemen)
Perhatikan gambar di bawah ini.
 Pada gambar di atas terlihat ∠PQR merupakan sudut siku-siku, sehingga besar ∠PQR = 90°. Jika pada ∠PQR ditarik garis dari titik sudut Q, akan terbentuk dua sudut, yaitu ∠PQS dan ∠RQS. Dalam hal ini dikatakan bahwa ∠PQS merupakan penyiku (komplemen) dari ∠RQS, demikian pula sebaliknya. Sehingga diperoleh:
Pada gambar di atas terlihat ∠PQR merupakan sudut siku-siku, sehingga besar ∠PQR = 90°. Jika pada ∠PQR ditarik garis dari titik sudut Q, akan terbentuk dua sudut, yaitu ∠PQS dan ∠RQS. Dalam hal ini dikatakan bahwa ∠PQS merupakan penyiku (komplemen) dari ∠RQS, demikian pula sebaliknya. Sehingga diperoleh:
Perhatikan gambar di bawah ini.

∠PQS + ∠RQS = ∠PQR
x° + y° = 90°,
dengan
x° = 90° – y° dan
y° = 90° – x°.
Dari uraian di atas dapat disimpulkan sebagai berikut. Jumlah dua sudut yang saling berpenyiku (berkomplemen) adalah 90°. Sudut yang satu merupakan penyiku dari sudut yang lain.
Dari uraian di atas dapat disimpulkan sebagai berikut. Jumlah dua sudut yang saling berpenyiku (berkomplemen) adalah 90°. Sudut yang satu merupakan penyiku dari sudut yang lain.
Contoh Soal
Perhatikan gambar di bawah.
Perhatikan gambar di bawah.
Berdasarkan gambar di atas hitunglah nilai x°; berapakah penyiku sudut x°; dan berapakah pelurus dari penyiku x°?
Penyelesaian:
x° + 3 x° = 90°
4 x° = 90°
x° = 22,5°
penyiku dari x° = 90° - 22,5° = 67,5°
pelurus dari penyiku x° = 180° - 67,5° = 112,5°
Pasangan Sudut yang Saling Bertolak Belakang
Perhatikan gambar di bawah ini.
 Pada gambar di atas, garis KM dan LN saling berpotongan di titik O. Dua sudut yang letaknya saling membelakangi disebut dua sudut yang saling bertolak belakang, sehingga diperoleh sudut KON bertolak belakang dengan sudut LOM; dan sudut NOM bertolak belakang dengan sudut KOL.
Pada gambar di atas, garis KM dan LN saling berpotongan di titik O. Dua sudut yang letaknya saling membelakangi disebut dua sudut yang saling bertolak belakang, sehingga diperoleh sudut KON bertolak belakang dengan sudut LOM; dan sudut NOM bertolak belakang dengan sudut KOL.
Bagaimana besar sudut yang saling bertolak belakang? Agar dapat menjawabnya, perhatikan uraian berikut.
Perhatikan gambar di bawah ini.

Bagaimana besar sudut yang saling bertolak belakang? Agar dapat menjawabnya, perhatikan uraian berikut.
∠KOL + ∠LOM = 180° (berpelurus)
∠LOM = 180° – ∠KOL ........................... (i)
∠NOM + ∠LOM = 180° (berpelurus)
∠LOM = 180° – ∠MON ......................... (ii)
Dari persamaan (i) dan (ii) diperoleh:
∠LOM = ∠LOM
180° – ∠KOL = 180° – ∠MON
∠NOM =∠KOL
Jadi, besar ∠KOL = besar ∠MON.

∠MON + ∠KON = 180° (berpelurus)
∠MON = 180° – ∠KON ........................... (a)
∠MON + ∠LOM = 180° (berpelurus)
∠MON = 180° – ∠LOM ......................... (b)
Dari persamaan (a) dan (b) diperoleh:
∠MON = ∠MON
180° – ∠KON = 180° – ∠LOM
∠LOM =∠KON
Jadi, besar ∠KON = besar ∠LOM.
Dari uraian di atas dapat disimpulkan sebagai berikut. Jika dua garis berpotongan maka dua sudut yang letaknya saling membelakangi titik potongnya disebut dua sudut yang bertolak belakang. Dua sudut yang saling bertolak belakang adalah sama besar.
Dari uraian di atas dapat disimpulkan sebagai berikut. Jika dua garis berpotongan maka dua sudut yang letaknya saling membelakangi titik potongnya disebut dua sudut yang bertolak belakang. Dua sudut yang saling bertolak belakang adalah sama besar.
Contoh Soal
Perhatikan gambar di bawah ini.
Diketahui besar ∠SOP = 45°. Tentukan besar ∠ROQ, ∠SOR, dan ∠POQ.Penyelesaian:
Diketahui:
∠SOP = 45°
∠SOP = 45°
∠ROQ = ∠SOP (bertolak belakang)
∠ROQ = 45°
∠ROQ = 45°
45° + ∠SOR = 180°
∠SOR = 180° – 45°
∠SOR = 135°
∠POQ = ∠SOR (bertolak belakang)
∠POQ = 135°


No comments:
Post a Comment